Es ist davon auszugehen, dass die
in der Galaxie vorhandenen Zivilisationen über die
gesamten geschichtlichen Entwicklungsstufen hinweg
verteilt sein werden. In einem ersten Ansatz könnte man
davon ausgehen, dass alle Zivilisationen gleichmäßig
über die Zivilisationsstufen verteilt sind.
Dagegen kann man aber anführen, dass je länger eine
Zivilisation besteht auch die Wahrscheinlichkeit einer
alles vernichtenden Katastrophe zunimmt. Es ist daher
eher zu erwarten, dass die Anzahl der Zivilisationen mit
steigender Entwicklungsstufe abnimmt. Daraus lässt sich
folgender Ansatz formulieren:
| 6.2.1
Ansatz |
Die Wahrscheinlichkeit Fz für eine
Zivilisation ist umgekehrt proportional zur
Entwicklungsstufe.
Fz = 1:m und m
= Entwicklungsstufe |
In der folgenden Grafik ist dies noch ein mal bildlich
dargestellt.
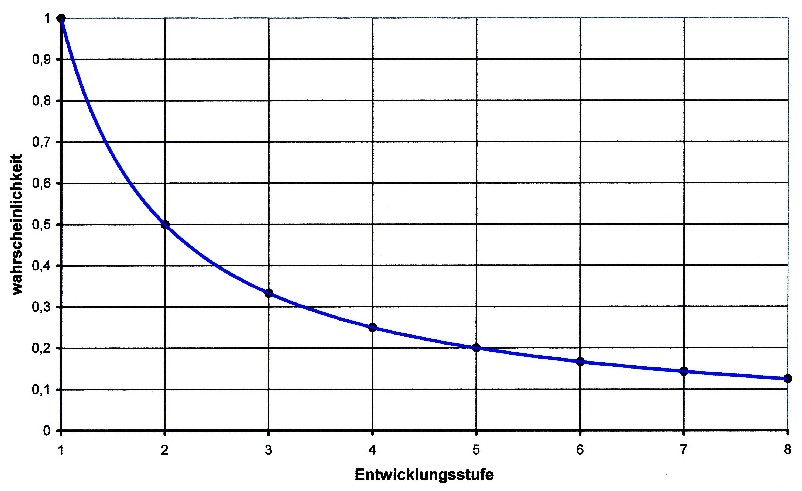
Wenn auf einem Planeten intelligentes Leben entstanden
ist, so ist es 100 % wahrscheinlich, dass auch Vorstufen
von Zivilisationen entstanden sind, eben solche der Stufe
1. Folglich liefert auch die Entwicklungsstufenfunktion
hier den Wert 1.
Aber schon bei Stufe 2 beträgt die Wahrscheinlichkeit
nur noch 0,5, bei Stufe 3 noch 0,33, bei Stufe 4 nur noch
0,25 usw.
Es muss jetzt noch gefordert werden, dass die Summe aller
Wahr-scheinlichkeiten für die Zivilisationsstufen (m
> 2) gleich eins ist. Das bedeutet, dass es 100 %
wahrscheinlich ist, dass über die Summe aller
Zivilisationsstufen gesehen, mindestens eine existiert.
Also gilt:
| 6.2.2
Gleichung |
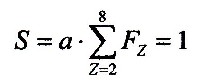 |
Das ist aber dem bisherigen Ansatz
6.2.1 nicht der Fall, denn die Summenbildung liefert:
S = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 +
1/8 = 481 : 280 > 1
Wahrscheinlichkeiten können aber nicht größer als eins
werden. Daher muss man einen verschärften Ansatz finden.
Ein besserer Ansatz lässt sich dadurch erreichen, dass
man das Quadrat der Entwicklungsstufe zur Berechnung der
Wahrscheinlichkeit Fz benutzt, also:
Fz
= 1:m2 und m
> 1 ist Entwicklungsstufe
Die Summenbildung liefert hier:
S = 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + 1/64
S = 7.301 : 14.400
S = 0,507.013
Dann lässt sich die Normierungsfunktion 6.2.2 so
modifizieren:
| 6.2.3
Gleichung |
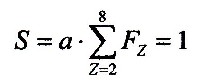 |
Um die Entwicklungsstufenfunktion anzupassen, muss der
Faktor a gleich dem Kehrwert der Summe sein, also:
a = 14.400 :
7.301
a = 1,972.332
Damit lässt sich jetzt folgender
Ansatz für die Wahrscheinlichkeit einer
Entwicklungsstufe aufstellen:
| 6.2.4
Gleichung |
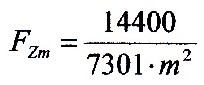 |
m >
1 |
In der nachfolgenden Grafik ist das noch einmal bildlich
dargestellt.
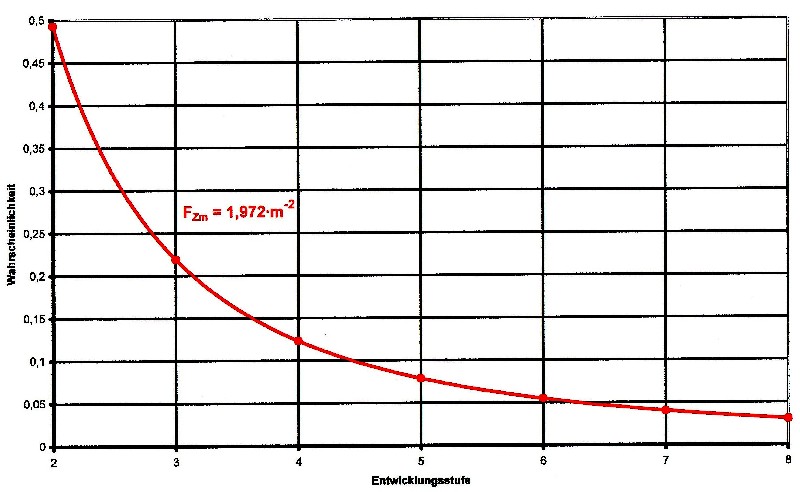
Durch die Entwicklungsstufenfunktion 6.2.4 lässt sich
noch die Gesamtwahrscheinlichkeit für alle
Zivililisationsstufen größer 2 ermitteln
Die Gesamtwahrscheinlichkeit wird durch die Fläche
dargestellt die sich unter der Funktion aufspannt. Man
muss also das Integral über der Funktion bilden. Das
lässt sich dann so formulieren:
Die Gesamtwahrscheinlichkeit für die Existenz einer
Zivilisation entspricht dem Integral über der
Wahrscheinlichkeitsfunktion einer Zivilisation.
| 6.2.5
Gleichung |
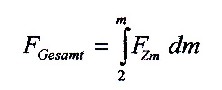 |
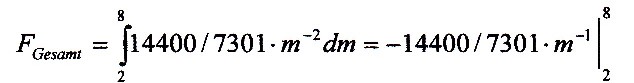
FGesamt = 14400/7301 ·
(-8-1 + 2-1)
FGesamt = 5400/7301 = 0,739.624
Das bedeutet, dass eine Gesamtwahrscheinlichkeit von etwa
74 % besteht, überhaupt eine Zivilisation anzutreffen.
Mit der Wahrscheinlichkeitsfunktion für
Zivilisationsstufen steht nun ein wirksames Werkzeug zur
Verfügung, die Wahrscheinlichkeiten für die
Entwicklungsstufen einer Zivilisation zu beschreiben und
einzuordnen.
Es muss jetzt nur noch eines vorausgesetzt werden:
| 6.2.6 Axiom |
Alle Betrachtungen zu den
Entwicklungsstufen, der Entwicklungszeit und der
Verteilung von Zivilisationsstufen sind auf
außerirdische Zivilisationen übertragbar. |
|